Answer:
The probability that it will weigh more than 904 grams = 0.9452
Explanation:
Given -
Mean
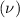 = 920 grams
= 920 grams
Standard deviation
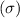 =10
=10
Let X be the weight of a certain brand of adult cereal
if we select one box of cereal at random from this population
The probability that it will weigh more than 904 grams =
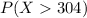 =
=
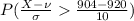
=
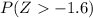 Putting
Putting
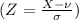
=
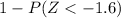 Using Z table
Using Z table
= 1 - .0548
= 0.9452