Question

A rectangle has a length 6 more than it’s width if the width is decreased by 2 and the length decreased by 4 the resulting has an area of 21 square units what is the length of the original rectangle what is ratio of the original rectangle area to the new rectangle area what is the perimeter of the new rectangle

Answer 1

Length of original rectangle is : x+6 = 5+6 = 11 units

ratio of the original rectangle area to the new rectangle area:
`(55)/(21)`

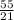
perimeter of the new rectangle : 2(x+2+x-2) = 4x = 4(5) = 20 units

Explanation:

Here we have , A rectangle has a length 6 more than it’s width if the width is decreased by 2 and the length decreased by 4 the resulting has an area of 21 square units what is the length of the original rectangle . We need to find what is ratio of the original rectangle area to the new rectangle area what is the perimeter of the new rectangle . Let's find out:

Initial parameters of rectangle are : Length = x+6 , width = x

width is decreased by 2 and the length decreased by 4 :

Length = x+6-4 = x+2 , width = x -2 , So area is :

⇒
`Area = Length(width)`

⇒
`21= (x+2)(x-2)`

⇒
`21= x^2-4`

⇒
`x^2=25`

⇒
`x=5`

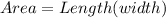
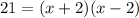
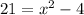
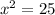
So , Length of original rectangle is : x+6 = 5+6 = 11 units

ratio of the original rectangle area to the new rectangle area:

⇒
`(11(5))/(7(3))`

⇒
`(55)/(21)`

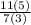
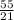
perimeter of the new rectangle : 2(x+2+x-2) = 4x = 4(5) = 20 units