Question

The proportion of supermarket customers who do not buy store-brand products is to be estimated. Which of the following scenarios would lead to a sampling distribution of the sample proportion with the lowest variability?

a Sample 100 customers from the roughly 2000 customers who shop at one store location.

b Sample 100 customers from the roughly 20,000 customers who shop at the stores citywide.

c Sample 200 customers from the roughly 2000 customers who shop at one store location.

d Sample 300 customers from the roughly 20,000 customers who shop at the stores citywide.

Answer 1

Option C

Explanation:

We have to minimize the standard error of the proportion.

We have a finite population (one for the customers who shop at one store location and other bigger that is for the customers who shop at the stores citywide).

The standard error for a finite population can be written as:

`\sigma_x=(s)/(√(n)) \sqrt{1-(n)/(N) }`

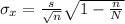
For each population, the higher the sample size, the less variablity will have in the estimation of the proportion. So, we are left with option C and D.

We can calculate the standard error for each posibility and compare:

c) Sample n=200 customers from the roughly N=2000 customers who shop at one store location.

`\sigma_x=(s)/(√(100))\sqrt{1-(200)/(2000) } \\\\ \sigma_x=(s)/(10) √(1-0.1 )=s(0.1*0.949)=0.0949s`

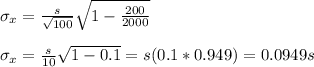
d) Sample 300 customers from the roughly 20,000 customers who shop at the stores citywide.

`\sigma_x=(s)/(√(100))\sqrt{1-(300)/(20000) } \\\\ \sigma_x=(s)/(10) √(1-0.015 )=s(0.1*0.992)=0.0992s`

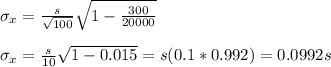
It will give less variability the Option C.

It is assumed that sampling only one store is representative of the parameter of the population of study.