Answer:
Length = 12 in
Width = 4 in
Height = 1.5 in
Explanation:
Let the side length of the squares that are cut off be x.
By cutting the squares off, the height of the box formed will be x.
The length will be the length of cardboard - 2x =
 .
.
The width will be the width of cardboard - 2x =
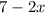
The volume is given by
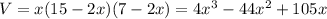
To maximize the volume,
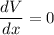
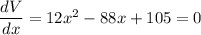
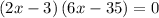
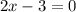 OR
OR
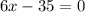
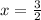 OR
OR
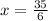
To determine which value of x gives a maximum, we evaluate
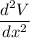
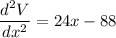
The value of x that gives a negative value is maximum.
At
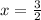 ,
,
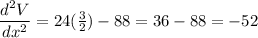
We can confirm the other value will be positive:
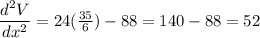
The maximum occurs when
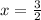 .
.
This corresponds to
height =
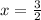
length =
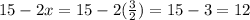
width =
