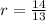Question

The equation of a circle is given below. x^{2}+(y-2.25)^{2} = \dfrac{196}{169}x 2 +(y−2.25) 2 = 169 196 ​ x, squared, plus, left parenthesis, y, minus, 2, point, 25, right parenthesis, squared, equals, start fraction, 196, divided by, 169, end fraction What is its center? ((left parenthesis ,,comma ))right parenthesis What is its radius

Answer 1

(0, 7.5)

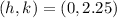
0.42- radius

Explanation:

Answer 2

• Center =
  `(h,k) = (0,2.25)`
• Radius =
  `r = (14)/(13)`

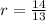
Explanation:

Here we have following equation :
`x^(2)+(y-2.25)^(2) = (196)/(169)`

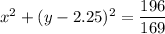
We need to find the center & radius of this circle . Let's find out:

We know that , Equation of a circle is given by :

⇒
`(x-h)^2+(y-k)^2=r^2` ........(1)

Here , (h,k) are the co-ordinates of center & r is the radius of circle.Collectively called as a circle with radius r and center at (h,k) . Let's frame given equation in question :

⇒
`x^(2)+(y-2.25)^(2) = (196)/(169)`

⇒
`(x-0)^(2)+(y-2.25)^(2) = ((14)/(13))^2`

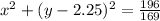
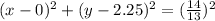
On comparing this equation with equation (1) we get :

• Center =
  `(h,k) = (0,2.25)`
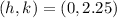
• Radius =
  `r = (14)/(13)`