Question

Porphyrin is a pigment in blood protoplasm and other body fluids that is significant in body energy and storage. In healthy Alaskan brown bears, the amount of porphyrin in the bloodstream (in mg/dl) has approximate normal distribution with mean 47.5 and a standard deviation 12.2.

a) What proportion of these bears have between 27.5 and 67.5 mg/dL porphyrin in their bloodstream? (That's within 20 of the mean amount of 47.5)
b) How low are the porphyrin levels for the lowest 3% of all the bears?

Answer 1

• a) 0.899

• b) less than or equal to 70.4 mg/dL

Step-by-step explanation:

You can work the probabilities of events that follow normal distributions with the tables of the cumulative areas for the standardized normal distribution.

First, you need to find the standardized values, this is the z-scores.

The z-score represents how much a value is away of the mean and is calculated with the formula:

`z-score=(x-\mu)/(\sigma)`

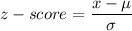
Where:

• x is the value of the variable,
• μ is the mean, and
• σ is the standard deviation

Part a)

Calculate the z-scores for both 27.5 and 67.5 mg/dL

`z_1=(27.5-47.5)/(12.2)=-1.64`

`z_2=(67.5-47.5)/(12.2)=1.64`

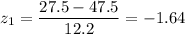
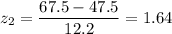
Then, you need to find the area under the curve of the standardized normal distribution between the z values -1.64 and 1.64.

From the corrsponding the table, the area to the right of z = 1.64, z ≥ 1.64, is = 0.0505.

The area to the right of z = -1.64, is 1 - 0.0505 = 0.9495

Thus, the area in between is 0.9495 - 0.0505 = 0.899, and that is the proportion of bears that have between 27.5 and 67.5 mg/dL porphyrin in their bloodstream.

Part b)

You need to find the z-score that corresponds to a proportion (probability) of 3%. That is 0.03.

In the table, you find that a 0.0301 probability corresponds to a z-score of 1.88 and 0.0294 corresponds to 1.89.

Then, you must interpolate:

`(z-1.88)/(0.03-0.0301)=(1.88-1.89)/(0.0301-0.0294)`

`z\approx1.881`

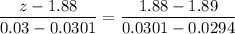
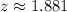
Now, you use the formula for z-score to solve for x:

`1.881=(x-47.5)/(12.2)`

`x=12.2* 1.881 + 47.5=70.4`

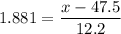
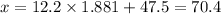
Then, the porphyrin levels of the lowest 3% of all the bears less than or equal to 70.4 mg/dL