Question

A quiz consists of 10 true or false questions. To pass the quiz a student must answer at least eight questions correctly.

If the student guesses on each question, what is the probability that the student will pass the quiz?

Answer 1

The probability of the student will pass the quiz = .0546

Explanation:

Given -

Total no of question = 10

If the student guesses on each question there are two outcomes true of false

the probability of guesses question correctly =
`(1)/(2)`

the probability of success is (p) =
`(1)/(2)`

the probability of guesses question incorrectly =
`(1)/(2)`

the probability of failure is (q) = 1- p =
`(1)/(2)`

If the student guesses on each question he must answered at least 8 question correctly

the probability of the student will pass the quiz =
`P(X\geq8 )`

= P(X = 8 ) + P(X = 9) + P(X = 10 )

=
`\binom{10}{8}(p)^(8)(q)^(10 - 8) + \binom{10}{9}(p)^(9)(q)^(10 - 9) + \binom{10}{10}(p)^(10)(q)^(10 - 10)`

=
`(10!)/((2!)(8!))((1)/(2))^(8)((1)/(2))^(10 - 8) +(10!)/((1!)(9!)) ((1)/(2))^(9)((1)/(2))^(10 - 9) + (10!)/((0!)(10!))((1)/(2))^(10)((1)/(2))^(10 - 10)`

=
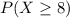
`45*(1)/(2^(10)) + 10*(1)/(2^(10)) + 1*(1)/(2^(10))`

=
`(56)/(2^(10))`

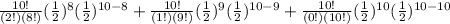
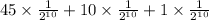
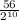
= .0546