Answer:
For the maximize the total area, the all wire i.e. 26 m should be used for the square.
Explanation:
Length of the wire = 26 m
Let Amount of wire cut for square = x
Amount of wire cut for triangle = 26 - x
Side of the square =
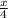
Area of the square =
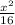 ------ (1)
------ (1)
Side of the triangle is given by
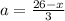
Side of the triangle is
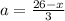
Area of the triangle is given by
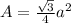
Area of the triangle is
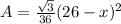 ------- (2)
------- (2)
Now the total area = Area of square + Area of triangle
The total area =
 ------- (3)
------- (3)
Differentiate above equation with respect to x we get
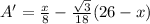
Take
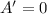
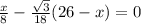 ------- (4)
------- (4)
By solving the above equation we get
x = 11.31 m
Again take
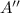 by differentiating equation (4)
by differentiating equation (4)

Which is greater than zero. so the value x = 11.31 m gives the area minimum.
Thus for the maximize the total area, the all wire i.e. 26 m should be used for the square.