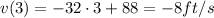A foul tip of a baseball is hit straight upward from a height of 4 feet with an initial velocity of 88 feet per second. The function s(t) = -16 t^2 + 88 t + 4 describes the​ bal…

Question

A foul tip of a baseball is hit straight upward from a height of 4 feet with an initial velocity of 88 feet per second. The function
`s(t) = -16 t^2 + 88 t + 4` describes the​ ball's height above the​ ground, ​s(t)​, in​ feet, t seconds after it was hit.What is the instantaneous velocity of the ball 1 second after it is hit? 3 seconds after it is hit?

Answer 1

at t = 1 s: +56 ft/s

at t = 3 s: -8 ft/s

Explanation:

The equation that describes the heigth of the ball at time t is

`s(t)=-16t^2+88t+4`

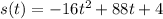
where

4 ft is the initial height at t = 0

+88 ft/s is the initial velocity of the ball

`-32 ft/s^2` is the acceleration due to gravity

The instantaneous velocity of the ball can calculated as the derivative of the position.

Calculating the derivative of s(t) with respect to time, we find an expression for the instantaneous velocity:

`v'(t)=(ds(t))/(dt)=-2\cdot 16 t^(2-1) +88 t^(1-1)+4\\\rightarrow v(t) = -32t+88`

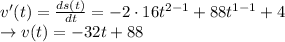
Now we can find the value of the instantaneous velocity at various times t:

- At t = 1 second, we have

`v(1)=-32\cdot 1 + 88 = 56 ft/s`

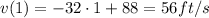
- At t = 3 seconds, we have

`v(3)=-32\cdot 3 + 88 =-8 ft/s`