Question

Outside temperature over a day can be modeled as a sinusoidal function. Suppose you know the temperature varies between 56 and 74 degrees during the day and the average daily temperature first occurs at 10 AM. How many hours after midnight, to two decimal places, does the temperature first reach 63 degrees

Answer 1

The temperature first reach 63 degrees at 9:09 AM.

Explanation:

We can write a model for the temperature during the day as:

`T(t)=Asin(\omega t+\phi)+B`

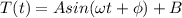
The minimum temperature is 56:

`T=A*(-1)+B=56\\\\B=56+A`

The maximum temperature is 74:

`T=A*1+B=A+(56+A)=74\\\\2A=(74-56)=18\\\\A=9\\\\B=56+A=65`

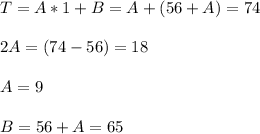
The cicle repeats daily, so T(0)=T(24). Other way to calculate it is that:

`\omega\cdot 24=2\pi\\\\\omega=\pi/12`

(2 pi is one cycle for the sin function).

The average temperature occurs when

`sin( (\pi)/(12) t+\phi)=0`

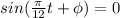
Then we, we calculate this for the 10 AM (t=10)

`sin( (\pi)/(12) \cdot 10+\phi)=0\\\\(\pi)/(12) \cdot 10+\phi=2\pi\\\\ \phi=(7)/(6) \pi`

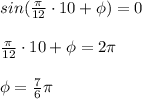
Then, we have all parameters calculated and the model is:

`T(t)=9sin((\pi)/(12)\cdot t+(7\pi)/(6) )+65`

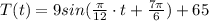
We hace to calculate how many hours after midnight, to two decimal places, does the temperature first reach 63 degrees

`T(t)=9sin((\pi)/(12)\cdot t+(7\pi)/(6) )+65 = 63\\\\9sin((\pi)/(12)\cdot t+(7\pi)/(6) ) = 63-65\\\\sin((\pi)/(12)\cdot t+(7\pi)/(6) ) = -2/9\\\\(\pi)/(12)\cdot t+(7\pi)/(6)=arcsin(-2/9)=6.06\\\\t=(6.06-7\pi/6)/(\pi/12)\\\\t= 9.144`

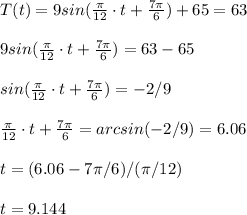
The value t=9.144 is equal to 9:09 AM.