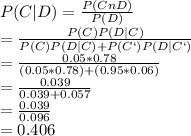Question

Referring to Exercise 2.95, what is the probability that a person diagnosed as having cancer actually has the disease?

Answer 1

The answer is 0.406

Explanation:

Exercise 2.95: In a certain region of the country it is known from past experience that theprobability of selecting an adult over 40 years of age with cancer is 0.05. If the probability of a doctor correctly diagnosing a person with cancer as having the disease is 0.78 and theprobability of incorrectly diagnosing a person without cancer as having the disease is 0.06,what is the probability that an adult over 40 years of age is diagnosed as having cancer?

This time we want to calculate P(C | D). To do this, we use Bayes rule:

`P(C | D) = (P(C n D))/(P(D)) \\= (P(C)P(D | C))/(P(C)P(D | C) + P(C`)P(D | C`)) \\= (0.05 * 0.78)/((0.05 * 0.78) + (0.95 * 0.06)) \\= (0.039)/(0.039 + 0.057) \\=(0.039)/(0.096) \\= 0.406`