Question

A 500-page book contains 250 sheets of paper. The thickness of the paper used to manufacture the book has a mean of 0.08 mm and a standard deviation of 0.01 mm.

a. What is the probability that a randomly chosen book is more than 20.2 mm thick (not including the covers)?
b. What is the 10th percentile of book thicknesses?
c. Someone wants to know the probability that a randomly chosen page is more than 0.1 mm thick. Is enough information given to compute this probability? If so, compute the probability. If not, explain why not.

Answer 1

`a. \ P(S>20.2)=0.103 \ \ or \ 10.3\%`

`b.\ \ S_(10)=19.797 \ mm\\\\c. \ No`

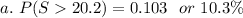
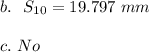
Explanation:

a. Let X be paper. the thickness .

Given the paper's parameters
`\mu=0.08,\ \ \ \sigma=0.01`

-Also, let S be the book's thickness.

The book's parameters are calculated as:

`\#mean\\\mu_s=n\sigma_p^2\\\\=250(0.08)=20.00\\\\\# Standard \ deviation, \sigma_s\\\sigma_s^2=250(0.01)^2=0.0250\\\\\sigma_s=√(0.025)=0.15811`

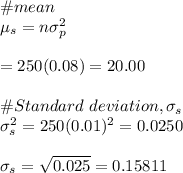
# the probability that a randomly chosen book is more than 20.2 mm thick is then calculated as:

`P(S>20.2)=P(z>(\bar x-\mu_s)/(\sigma_s))}\\\\=P(z>(20.2-20.0)/(0.15811))\\\\=P(z>1.26494)\\\\=1-P(<1.26494)\\\\=0.102952 \ \ or \ 10.3%`

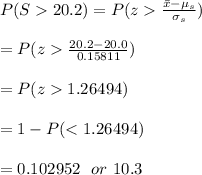
Hence, the probability is 0.103 or 10.3%

b. let's denote the 10th percentile as
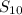`S_(10)`, for the book's thickness.

From a above, we have the mean for the book's thickness as
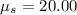`\mu_s=20.00` and the variance as
`\sigma_s^2=0.025`.

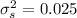#We therefore calculate the 10th percentile as;

`P(S<S_(10))=10\%=0.10\\\\P(z<-1.282)=0.1\\\\S_(10)+\mu_s+z\sigma_s\\\\=20.00+(-1.282)(0.15811)\\\\=19.797`

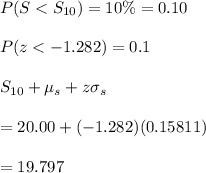
Hence, the 10th percentile of the book's thickness is 19.797 mm

c.No.

-This is because the distribution of the book's thickness is not known.

-Hence, this probability cannot be calculated.