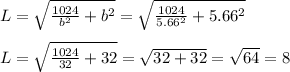Question

A rectangle has area 64 cm^2. A straight line is to be drawn from one corner of the rectangle to the midpoint of one of the two more distant sides. What is the minimum possible length of such a line

Answer 1

The minimum possible length of such a line is 8 cm

Explanation:

If we had a rectangle, we can name each side "a" and "b".

The area of the rectangle will be:

`S=a\cdot b = 64`

Note: This is the constraint of our optimiztion problem.

Applying the Pitagoras theorem, the line, as in the figure attached, will have a length of:

`L=√((a/2)^2+b^2)=\sqrt{a^2/4+b^2`

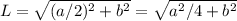
We can replace "a" as a function of "b":

`ab=64\\\\a=64/b`

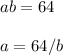
Then,

`L=\sqrt{(1)/(4)((64)/(b) )^2 +b^2}=\sqrt{(1024)/(b^2) +b^2`

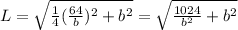
To calculate the minimum length, we derive and equal to zero:

`dL/db=(d)/(db) [((1024)/(b^2)+b^2)^{(1)/(2)} ]\\\\dL/db=(1)/(2) ((1024)/(b^2)+b^2)^{(-(1)/(2))}\cdot (d)/(db) [(1024)/(b^2)+b^2]\\\\ dL/db=\frac{2b+1024\cdot(-2)\cdot b^(-3)}{2\sqrt{((1024)/(b^2)+b^2)}} \\\\\\ dL/db=\frac{2b-2048\cdot b^(-3)}{2\sqrt{((1024)/(b^2)+b^2)}}`

`dL/db=\frac{2b-2048\cdot b^(-3)}{2\sqrt{((1024)/(b^2)+b^2)}}=0\\\\\\2b-2048b^(-3)=0\\\\2b=(2048)/(b^3)\\\\b^4=(2048)/(2) =1024\\\\b=\sqrt[5]{1024}\approx5.66`

Now, we know that one side is 5.66 cm.

Then, the other side should be:

`a=64/b=64/5.66=11.31`

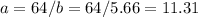
The length of the line for this side dimensions will be:

`L=\sqrt{(1024)/(b^2) +b^2}=\sqrt{(1024)/(5.66^2) +5.66^2}\\\\L=\sqrt{(1024)/(32) +32}=√(32+32)=√(64)=8`