Question

A humanities professor assigns letter grades on a test according to the following scheme. A: Top 12%12% of scores B: Scores below the top 12%12% and above the bottom 62%62% C: Scores below the top 38%38% and above the bottom 17%17% D: Scores below the top 83%83% and above the bottom 7%7% F: Bottom 7%7% of scores Scores on the test are normally distributed with a mean of 75.275.2 and a standard deviation of 9.89.8. Find the minimum score required for an A grade. Round your answer to the nearest whole number, if necessary.

Answer 1

The minimum score required for an A grade is 86.8.

Explanation:

We are given that a humanities professor assigns letter grades on a test according to the following scheme. A: Top 12% of scores B: Scores below the top 12% and above the bottom 62% C: Scores below the top 38% and above the bottom 17% D: Scores below the top 83% and above the bottom 7% E: Bottom 7% of scores

Scores on the test are normally distributed with a mean of 75.2 and a standard deviation of 9.8.

Let X = Scores on the test

SO, X ~ N(
`\mu = 75.2,\sigma^(2) = 9.8^(2)`)

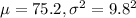The z-score probability distribution is given by ;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = mean score = 75.2

`\sigma` = standard deviation = 9.8

Now, the minimum score required for an A grade to be in the top 12% of scores is given by ;

P(X
`\geq`
`x` ) = 0.12 {where
`x` is the minimum score required}

P(
`(X-\mu)/(\sigma)`
`\geq (x-75.2)/(9.8)` ) = 0.12

P(Z
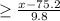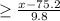`\geq (x-75.2)/(9.8)` ) = 0.12

Now, in z table we will find out that critical value of X for which the area is in top 12%, which comes out to be 1.1835.

This means;
`(x-75.2)/(9.8) = 1.1835`

`x-75.2=1.1835 * 9.8`

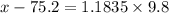
`x` = 75.2 + 11.5983 = 86.8

Therefore, the minimum score required for the scholarship is 86.8.