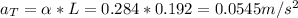Question

An 19.2-cm-long bicycle crank arm, with a pedal at one end is attached to a 20.6-cm-diameter sprocket, the toothed disk around which the chain moves. A cyclist riding this bike increases her pedaling rate from 57 rpm to 86 rpm in 10.7 s. What is the tangential acceleration of the pedal?

Answer 1

Tangential acceleration=
`a_(t)`=0.029233 m/s^2

Explanation

tangential acceleration=
`\alpha *r`

`\alpha`=ω/t

alpha=2
`\pi`((86/60)-(57/60))/10.7

`\alpha`=0.2838 m/s^2

at=
`\alpha`*r

radius=d/2=20.6/2=10.3 cm=0.103 m

at=0.2838*0.103=0.029233 m/s^2

Answer 2

0.0545 m/s2

Step-by-step explanation:

19.2 cm = 0.192 m

We can convert rpm (revolution per minute) to angular velocity rad/s knowing that each revolution is 2π rad and each minute is 60 seconds.

57 rpm = 57 * 2π / 60 = 6 rad/s

86 rpm = 86 * 2π / 60 = 9 rad/s

The angular acceleration of the sprocket is the change in angular velocity per unit of time

`\alpha = (\Delta \omega)/(\Delta t) = (9 - 6)/(10.7) = 0.284 rad/s^2`

The tangential acceleration of the pedal is the product of its angular acceleration and the radius of rotation, aka the pedal arm length L = 0.192 m

`a_T = \alpha*L = 0.284*0.192 = 0.0545 m/s^2`