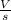Answer:
The time rate of change of flux is

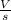
Step-by-step explanation:
Given :
Current
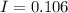 A
A
Area of plate
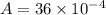

Plate separation
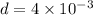 m
m
(A)
First find the capacitance of capacitor,
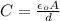
Where

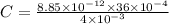
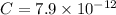 F
F
But
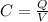
Where
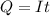
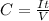
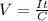
Now differentiate above equation wrt. time,
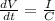
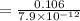

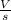
Therefore, the time rate of change of flux is