Question

) Assume that the heights of men are normally distributed with a mean of 66.8 inches and a standard deviation of 2.8 inches. If 64 men are randomly selected, find the probability that they have a mean height greater than 67.8 inches.

Answer 1

The probability that they have a mean height greater than 67.8 inches is 0.00212.

Explanation:

We are given that the heights of men are normally distributed with a mean of 66.8 inches and a standard deviation of 2.8 inches.

64 men are randomly selected.

Let
`\bar X` = sample mean height

The z-score probability distribution for sample mean is given by;

Z =
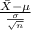`\frac{ \bar X -\mu}{{(\sigma)/(√(n) ) }} }` ~ N(0,1)

where,
`\mu` = mean height = 66.8 inches

`\sigma` = standard deviation = 2.8 inches

n = sample of men = 64

The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.

So, probability that they have a mean height greater than 67.8 inches is given by = P(
`\bar X` > 67.8 inches)

P(
`\bar X` > 67.8) = P(
`\frac{ \bar X -\mu}{{(\sigma)/(√(n) ) }} }` >
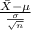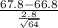`\frac{ 67.8 - 66.8}{{(2.8)/(√(64) ) }} }` ) = P(Z > 2.86) = 1 - P(Z
`\leq` 2.86)

= 1 - 0.99788 = 0.00212

The above probability is calculated by looking at the value of x = 2.86 in the z table which has an area of 0.99788.

Therefore, if 64 men are randomly selected, the probability that they have a mean height greater than 67.8 inches is 0.00212.