Question

In a lab experiment, 720 bacteria are placed in a Petri dish. The conditions are such that the number of bacteria is able to double every 26 hours. How long would it be, to the nearest 10th of an hour until there are 1310 bacteria present?

Answer 1

22.5 hours

Explanation:

Answer 2

22.4 hours

Explanation:

The population of bacteria is modelled by the equation:

`P=P_0e^(rt)`

From the the question, the initial population of bacteria is 720.

So after 26 hours, we have:

`P=2P_0`

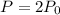
This implies that:

`2P_0=P_0e^(26r)`

`2=e^(26r)`

`26r = ln(2)`

`r = ( ln(2) )/(26)`

`r = 0.0267`

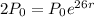
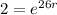
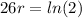
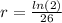
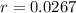
We want to find how long it will take for there to be 1310 bacteria present.

`1310=720e^(0.0267t)`

`(1310)/(720) = {e}^(0.0267t)`

`\ln((1310)/(720)) = {0.0267t}`

`0.59853= {0.0267t} \\ t = (0.59853)/(0.0267)`

`t = 22.417`

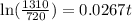
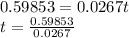
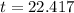
To the nearest tenth , it will take 22.4 hours