Question

I need too find the area of a triangle with variable sides. Base of (8x-7)inches, height of (6x) inches

Answer 1

The area of the given triangle is
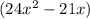`(24x^(2) - 21x)` square inches.

Explanation:

Step 1:

The area of a triangle is half the product of its base length and height.

The base is the lower end of the triangle and its length is called base length.

The length from the base to the highest point on the triangle is the height.

Step 2:

For the given triangle, the base extends for a length of (8x - 7) inches and the height is 6x inches.

The area of the given triangle
`= (1)/(2) (8x-7)(6x) = (1)/(2) (48x^(2) - 42x),`

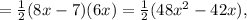
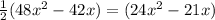`(1)/(2) (48x^(2) - 42x) = (24x^(2) - 21x)` square inches.

So the area of the given triangle is
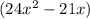`(24x^(2) - 21x)` square inches.