Answer:
95% confidence interval for the proportion of people in the population being treated for hypertension is [0.3293 , 0.3607].
Explanation:
We are given that during the 7th examination of the Offspring cohort in the Framing ham Heart Study, there were 1219 participants being treated for hypertension and 2,313 who were not on treatment.
So, the sample proportion is :
 = x/n = 1219/3532 = 0.345
= x/n = 1219/3532 = 0.345
Firstly, the pivotal quantity for 95% confidence interval for the proportion of the people in the population is given by;
P.Q. =
 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion = 0.345
= sample proportion = 0.345
n = sample of participants = 1219 + 2313 = 3532
p = population proportion
Here for constructing 95% confidence interval we have used One-sample z proportion statistics.
So, 95% confidence interval for the population proportion, p is ;
P(-1.96 < N(0,1) < 1.96) = 0.95 {As the critical value of z at 2.5% level of
significance are -1.96 & 1.96}
P(-1.96 <
 < 1.96) = 0.95
< 1.96) = 0.95
P(
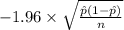 <
<
 <
<
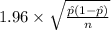 ) = 0.95
) = 0.95
P(
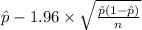 < p <
< p <
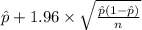 ) = 0.95
) = 0.95
95% confidence interval for p= [
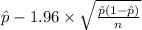 ,
,
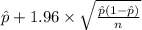 ]
]
= [
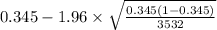 ,
,
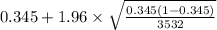 ]
]
= [0.3293 , 0.3607]
Hence, 95% confidence interval for the proportion of people in the population being treated for hypertension is [0.3293 , 0.3607].