Question

A satellite of mass ms travels in a circular orbit of radius a around a planet of mass mp?ms.

Part A

Derive expressions for the orbital speed of a satellite.

Express your answer in terms of some or all of the variables mp, ms, a, and gravitational constant G.

vs =

Answer 1

Orbital speed of the satellite is
`(√(Gm_p) )/(a)` .

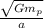Step-by-step explanation:

Given:

Gravitational constant =
`G`

Mass of the satellite =
`m_s`

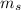
Mass of the planet =
`m_p`

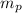
Radius of the orbit =
`a`

We have to derive the expressions for the orbital speed.

Let the orbital speed be 'vs'.

According to the question:

Force between the planet and the satellite.

From universal law of gravitation.

⇒
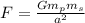`F=(Gm_pm_s)/(a^2)` ...equation (i)

And

Their is centripetal force acting towards the planet.

And we know centripetal acceleration
`a_c` =
`(v^2)/(r)` .

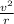From Newtons second law.

⇒
`F=ma`

⇒
`F=m(v^2)/(r)`

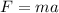
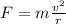
Here the velocity is vs and r = a and mass of the satellite is ms.

⇒
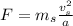`F=m_s(v_s^2)/(a)` ...equation (ii)

Equating both the equations.

equation (i) = equation (ii)

⇒
`(Gm_pm_s)/(a^2) = m_s(v_s^2)/(a)`

⇒
`(Gm_p)/(a) =v_s^2`

⇒
`\sqrt{(Gm_p)/(a) } =v_s`

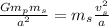
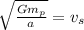
So,

The orbital speed of the satellite is Sq-rt(Gm_p/a).