Question

A neighborhood transformer on the top of a utility pole transforms 12.0 kV 60.0 Hz alternating voltage down to 120.0 V to be used inside a house. If the secondary coil of the transformer has 134.0 turns, then how many turns does the primary coil have

Answer 1

The primary coil has 13,400 turns

Step-by-step explanation:

Voltage Transformers

A transformer is an electrical apparatus that converts an alternating electrical voltage to another. Step-down transformers lower the voltage from higher levels (kilovolts) to consumer levels (120/240 Volts).

The ratio between both voltages can be computed as

`\displaystyle r=(V_1)/(V_2)`

Where V1 is the primary voltage and V2 is the secondary voltage. This ratio depends on the turns ratio of the coils wounded in a common magnetic core.

`\displaystyle r=(N_1)/(N_2)`

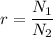
Being N1 the number of turns of the coils of the primary side and N2 the number of turns in the secondary coil. Both relations give us

`\displaystyle (N_1)/(N_2)=(V_1)/(V_2)`

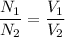
Solving for N1

`\displaystyle N_1=(V_1)/(V_2)\cdot N_2`

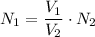
We have:

`V_1=12,000\ V\\V_2=120\ V\\N_2=134`

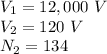
Calculate N1

`\displaystyle N_1=(12,000)/(120)\cdot 134=13,400`

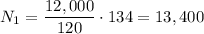
The primary coil has 13,400 turns