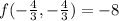Answer:
Therefore the absolute maximum value is
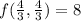
the absolute minimum value is
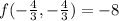
Explanation:
Method of Lagrange multipliers:
1. Solve the following system of equation

2. Plug the all solution (x,y,..) from the first step into f(x,y,..) and identify the maximum and minimum values.
The constant
 is known as the Lagrange Multiplier.
is known as the Lagrange Multiplier.
Given function is
f(x,y)= 3x+3y
subject to constrain
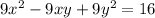
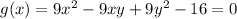
The partial derivatives are
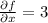
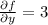
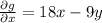
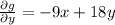
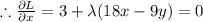 ......(1)
......(1)
 ......(2)
......(2)
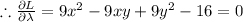 .....(3)
.....(3)
Multiplying 2 with equation (2) and add with equation (1)
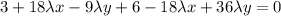
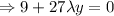
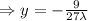
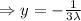
Putting the value of y in equation (1)
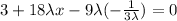
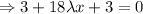
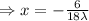

Putting the value of x and y in equation (3)
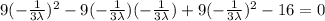


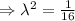

Therefore the value of x and y becomes

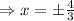
and
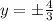
Therefore
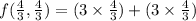
=4+4
=8
![f(-(4)/(3),-\frac43) =[3* (-\frac43)]+[3*(- \frac43)]](https://img.qammunity.org/2021/formulas/mathematics/college/tmitwyoa6dawtlaur08b2556sm9mruhiq6.png)
=-4-4
=-8
Therefore the absolute maximum value is
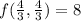
the absolute minimum value is