Answer:
1)
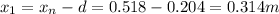
2)
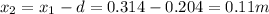
3)
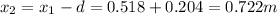
4)
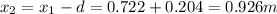
Step-by-step explanation:
Let's recall that two antinodes are required for a complete wavelength in standing waves which are produced by the facing speakers.
The equation for the spacing between two nodes of a stationaty wave is:
 (1)
(1)
Now, we know that velocity of a sound wave is:
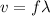 (2)
(2)
We can solve the equation 1 for λ and put it on equation 2
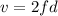

The antinode is formed in the half distance between both speakers, so:
x = 1.24/2 = 0.62 m
The location of the node will be:
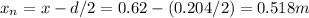
Therefore the nodes will be:
1)
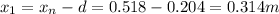
2)
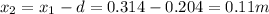
3)
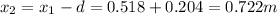
4)
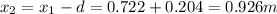
I hope it helps you!