Solutions of
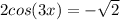 in the interval from [0,2pi) is
in the interval from [0,2pi) is
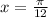 and
and
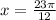 .
.
Explanation:
Find all solutions in the interval from [0,2pi)
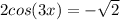
⇒
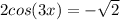
⇒
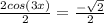
⇒
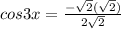
⇒
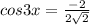
⇒
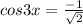
⇒
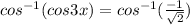
⇒

⇒
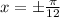
Cosine General solution is :
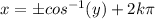
⇒
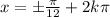 , k is any integer .
, k is any integer .
At k=0,
⇒
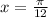 ,
,
At k=1,
⇒

⇒
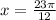
Therefore , Solutions of
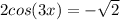 in the interval from [0,2pi) is
in the interval from [0,2pi) is
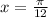 and
and
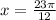 .
.