Answer:
Required side of the squire is
 , correct upto four desimal places.
, correct upto four desimal places.
Explanation:
Given two inequalities are,


which are reflexions of each other across the
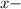 axis. And the square is inscribed within it. Since by symmetry, vertices of the square lies on the lines,
axis. And the square is inscribed within it. Since by symmetry, vertices of the square lies on the lines,

and
 . We only have to find length of any one side of the squire.
. We only have to find length of any one side of the squire.
To find
 , substitute
, substitute
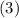 in
in
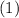 we get,
we get,
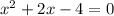
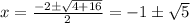
Since
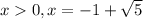 and from
and from
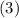 ,
,
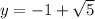 , and thus,
, and thus,
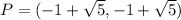
Similarly by substitute
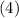 and
and
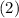 we will get,
we will get,
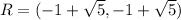
And thus,
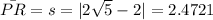 , correct upto four desimal places.
, correct upto four desimal places.