Question

Find values of a, b, and c (if possible) such that the system of linear equations has a unique solution, no solution, and infinitely many solutions. (If not possible, enter IMPOSSIBLE.)x + y = 4 y + z = 4x + z = 4ax + by + cz = 0

Answer 1

Explanation:

Given are four equations in three variables as

`x + y = 4 \\y + z = 4\\x + z = 4\\ax + by + cz = 0`

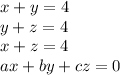
Let us take first three equations and solve

When we add we get 2(x+y+z) = 12

x+y+z = 6

Subtract from this equation the I equation to get z =2, similarly x =2, and y =2

If this is to be consistent with 4th equation we must have

2a+2b+2c =0

i.e. a +b+c =0

i.e. a =a, b =b and c = -a-b

Thre are infinite values for a,b,c to have x,y,z have solution as (2,2,2)

The system cannot have no solution or infinitely many solutions.