Question

Is 3 a primitive root of 7? If your answer is ‘yes’, you must show all computations that prove this result. If your answer is ‘no’, you must show sufficient computations to prove your answer.

Answer 1

Yes, 3 is a primitive root of 7.

Explanation:

By definition if primitive root, b is a primitive root of p, where p is a prime, if powers of b includes all residue classes mod p. Here,

`3^0=1`
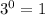
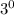`3^0` mod 7=1

`3^1=3`
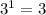
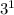`3^1` mod 7=3

`3^2=9`
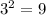
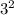`3^2` mod 7=2

`3^3=27`
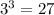
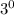`3^0` mod 7=6

`3^4=81`
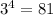
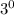`3^0` mod 7=4

`3^5=243`
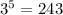
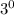`3^0` mod 7=5

And
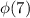`\phi(7)`=numbers less than 7 and prime to 7=1,2,3,4,5,6, presents in the residue class of 3 mod 7, this proves 3 is a primitive root of 7.