Complete Question
A cylinder with a moment of inertia I (about its axis of symmetry), mass m, and radius r has a mass-less string wrapped around it which is tied to the ceiling .
At time t=0 the cylinder is released from rest at height h above the ground. Use g for the magnitude of the acceleration of gravity. Assume that the string does not slip on the cylinder. Let v represent the instantaneous velocity of the center of mass of the cylinder, and let
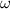 represent the instantaneous angular velocity of the cylinder about its center of mass. Note that there are no horizontal forces present, so for this problem
represent the instantaneous angular velocity of the cylinder about its center of mass. Note that there are no horizontal forces present, so for this problem
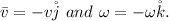
Expressions have been found for the vertical acceleration of the cylinder
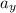 and the angular acceleration α of the cylinder in the k^ direction; both expressions include an unknown variable, namely, the tension T in the vertical section of string. The string constrains the rotational and vertical motions, providing a third equation relating
and the angular acceleration α of the cylinder in the k^ direction; both expressions include an unknown variable, namely, the tension T in the vertical section of string. The string constrains the rotational and vertical motions, providing a third equation relating
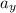 and α. Solve these three equations to find the vertical acceleration,
and α. Solve these three equations to find the vertical acceleration,
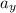 , of the center of mass of the cylinder. Express
, of the center of mass of the cylinder. Express
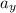 in terms of g, m, r, and I; a positive answer indicates upward acceleration.
in terms of g, m, r, and I; a positive answer indicates upward acceleration.
Answer:
The vertical acceleration is
![a_y = (mg)/([m+ (I)/(r^2) ])](https://img.qammunity.org/2021/formulas/physics/college/uiyyl2nljf7qyxtegvo62ovv26kvpf7lwc.png)
Step-by-step explanation:
The equation of motion is mathematically represented as
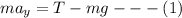
The relation between the tension and the moment of inertia is
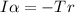
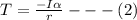
Now angular acceleration can be mathematically represented as
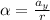
Now substituting this into equation 2
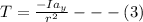
Now substituting these into equation 1
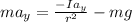
![a_y [m + (I)/(r^2) ] = -mg](https://img.qammunity.org/2021/formulas/physics/college/mpmnmrmnwygqeun99wqcyzjnqx7skm3ile.png)
Hence the vertical acceleration is evaluates as
![a_y = (mg)/([m+ (I)/(r^2) ])](https://img.qammunity.org/2021/formulas/physics/college/uiyyl2nljf7qyxtegvo62ovv26kvpf7lwc.png)