Question

A biker notices a mountain directly in front of her and determines that the angle of elevation to the summit is 3.5. After hiking 15 miles toward the mountain she records that the angle of elevation is 11. How tall is the mountain? Round the height to the nearest hundredth of a mile

Answer 1

The mountain is 1.34 miles tall.

Explanation:

See the attached diagram.

The height of the mountain is h miles (say).

Now, from the right triangle Δ ABC,

`\tan 3.5^(\circ) = (AB)/(AC) = (h)/(x + 15)`

⇒
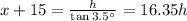`x + 15 = (h)/(\tan 3.5^(\circ)) = 16.35h` ........... (1)

Again, from the right triangle Δ ABD,

`\tan 11^(\circ) = (AB)/(AD) = (h)/(x)`

⇒
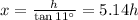`x = (h)/(\tan 11^(\circ)) = 5.14h` ............. (2)

Now, solving equations (1) and (2) we get,

15 = (16.35 - 5.14)h = 11.2h

⇒ h = 1.34 miles (To the nearest hundredth of a mile)

Therefore, the mountain is 1.34 miles tall. (Answer)