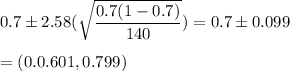Question

Use the normal distribution to find a confidence interval for a proportion P given the relevant sample results. Give the best point estimate for P, the margin of error and the confidence interval. Assume the results come from a random sample.

A 99% confidence interval for P given that p^ = 0.7 and n = 140.
Determine the following. Round your answer for the point estimate to two decimal places and your answers for the margin of error and the confidence interval to three decimal places.
(a) Point estimate
(b) Margin of error
(c) 99% confidence interval

Answer 1

a) 0.7

b) 0.075

c) (0.0.601,0.799)

Explanation:

We are given the following in the question:

`\hat{p} = 0.7`

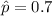
Sample size, n = 140

(a) Point estimate

The best point estimate for population proportion is the sample proportion.

`p = \hat{p} = 0.7`

(b) Margin of error

Formula:

`z_(stat)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`z_(critical)\text{ at}~\alpha_(0.05) = 1.96`

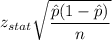
Putting values, we get,

Margin of error =

`1.96\sqrt{(0.7(1-0.7))/(140)} = 0.075`

(c) 99% confidence interval

`\hat{p}\pm z_(stat)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`z_(critical)\text{ at}~\alpha_(0.01) = \pm 2.58`

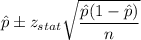
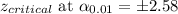
Putting the values, we get:

`0.7\pm 2.58(\sqrt{(0.7(1-0.7))/(140)}) = 0.7\pm 0.099\\\\=(0.0.601,0.799)`