Question

Which property would be useful in proving that the product of two rational numbers is ALWAYS rational? A) a b + c d = ad + bc bd B) a + b cd = a cd + b cd C) a b · c d = ac bd D) a b ÷ c d = a b · d c

Answer 1

Which property would be useful in proving that the product of two rational numbers is ALWAYS rational?

A) ab+ cd= ad + bcbd

B) a + bcd= acd+ bcd

C) ab· cd= acbd

D) ab÷ cd= ab· dc

Explanation:

Answer 2

C

Explanation:

So we need to understand what is rational numbers?

Rational number which can be written under this form:
`(x)/(y)` when x any are both integers and y
`\\eq 0`

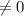
The question here is : Which property would be useful in proving that the product of two rational numbers. In math, when we talk about the product of at least two number, it implies to the multiplication in the operation.

Here, only answer C:
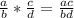`(a)/(b) *(c)/(d) = (ac)/(bd)` with the condition
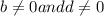`b\\eq 0 and d \\eq 0` and a, b, c and d are integers. Product of two integers is always an integer..