Question

(1 point) Find a linearly independent set of vectors that spans the same subspace of R3R3 as that spanned by the vectors ⎡⎣⎢3−1−2⎤⎦⎥, ⎡⎣⎢−923⎤⎦⎥, ⎡⎣⎢−30−1⎤⎦⎥. [3−1−2], [−923], [−30−1]. A linearly independent spanning set for the subspace is:

Answer 1

Step-by-step explanation:

`A=\left[\begin{array}{ccc}3&-9&-3\\-1&2&0\\-2&3&-1\end{array}\right] \\\\R_2\rightarrow 3R_2+R_1,R_3\rightarrow 3R_3+2R_1\\\\=\left[\begin{array}{ccc}3&-9&-3\\0&-3&-3\\0&-9&-9\end{array}\right] \\\\R_3\rightarrow 3R_3-9R_2\\\\=\left[\begin{array}{ccc}3&-9&-3\\0&-3&-3\\0&0&0\end{array}\right]`

This is the row echelon form of A. This means that only two of the vectors in our set are linearly independent. In other words, the first two vectors alone will span the same subspace of
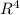`R^4` as all three vectors.

Therefore, the linearly independent spanning set for the subspace is

`\left[\begin{array}{ccc}3\\-1\\-2\end{array}\right] \left[\begin{array}{ccc}-9\\2\\3\end{array}\right] \left[\begin{array}{ccc}3\\0\\-1\end{array}\right]`