Question

What did they do wrong in this equation?

Look at the work for the following function. What mistake did they make when using the quadratic formula to find the solutions? What are the real solutions to the function?
​
​ f(x)=x2−9x+20
​Step 1: 9±−92−4(1)(20)√2(1)
​Step 2: 9±−81−80√2
​Step 3: 9±−161√2
​Step 4: There are no real solutions.

Answer 1

The real solutions to the function is x = ±5 .

Explanation:

Here we have following info: Look at the work for the following function. What mistake did they make when using the quadratic formula to find the solutions? What are the real solutions to the function?

​ Let's check step by step:

​
`f(x) = x^2-9x+20`

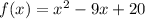
​Step 1: 9±−92−4(1)(20)√2(1)

Formula is :
`x = (-b + √(b^2-4ac) )/(2a)`

⇒
`x = (-(-9) + √((-9)^2-4(1)(20)) )/(2(1))`

⇒
`x = (9 + √(81-80) )/(2(1))`

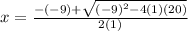
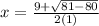
​Step 2: 9±−81−80√2

`x = (9 + √(81-80) )/(2(1))`

`x = (9 + √(1) )/(2)`

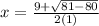
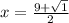
​Step 3: 9±−161√2

Mistake here is instead of subtracting , 81 & 80 are added!

`x = (9 + √(1) )/(2)`

`x = (10)/(2) = 5`

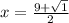
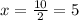
More precisely , x = ±5

​Step 4: There are no real solutions.

Wrong statement!

∴The real solutions to the function is x = ±5 .