Answer:
The rate of change of the length of the diagonal
 is
is
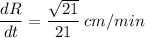
Explanation:
For the box of length
 , width
, width
 , and height
, and height
 , the length of the diagonal
, the length of the diagonal
 is given by
is given by
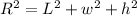 ,
,
Taking the time derivative of both sides we get:
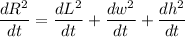
since for any function

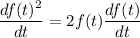 ,
,
our equation becomes
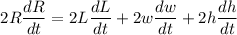
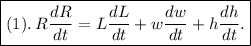
Now, at a certain time when
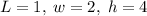 , the length of the diagonal is
, the length of the diagonal is
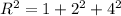
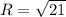 ,
,
and since
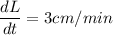
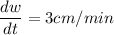
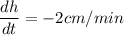
equation (1) becomes
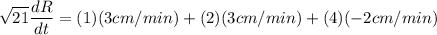
![$√(21) (dR)/(dt) =[3+6 +(-8)]\:cm/min$](https://img.qammunity.org/2021/formulas/mathematics/high-school/hv6b63741qs5um84ki47wriq3nuj43iqna.png)
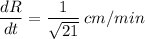
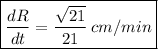
or
