Answer:
53.35 AU
Step-by-step explanation:
Using Kelper's third law
The relation between the time period (T) and the semi-major axis of the comet can be expressed as:
T²∝a³
T² = Ka³
where;
(a) = length of the semi-major axis
Making (a) the subject of the axis
a³
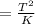
![a = \sqrt[3]{(T^2)/(K) }](https://img.qammunity.org/2021/formulas/geography/college/rgrrqe5wqtubrrabwm6771dq999c676whx.png)
![a = \sqrt[3]{(((137.6y)((3.16*10^7sec)/(1year))^2)/(2.96*10^(-19)s^2/m^3) }](https://img.qammunity.org/2021/formulas/geography/college/1lorpxwgn29bse19lf8dffjpo0nqhbcx9r.png)

a = 26.72 AU
Finally, the greatest distance from the Sun is:
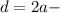
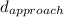
d = 2(26.72) - 0.09
d =53.44 - 0.09
d = 53.35 AU
Thus, the greatest distance from the Sun = 53.35 AU