Question

A tire manufacturer would like to estimate the average tire life of its new​ all-season light truck tire in terms of how many miles it lasts. Determine the sample size needed to construct a 98​% confidence interval with a margin of error equal to 3 comma 000 miles. Assume the standard deviation for the tire life of this particular brand is 9 comma 000 miles. The sample size needed is nothing. ​(Round up to the nearest​ integer.)

Answer 1

Sample size of at least 49 must be needed .

Explanation:

We are given that a 98​% confidence interval is constructed with a margin of error equal to 3,000 miles. Assume the standard deviation for the tire life of this particular brand is 9,000 miles.

So, Margin of error formula is given by =
`Z_(\alpha)/(2)* (\sigma)/(√(n) )`

where,
`\alpha` = significance level which is 2%

`\sigma` = standard deviation = 9,000 miles

n = sample size

Here, the value of z score at 2% significance level is 2.3263 .

So, margin of error = 2.3263 *
`(9000)/(√(n) )`

`√(n)` =
`(2.3263*9000)/( 3000)`

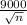
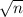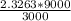
= 6.9789

n =
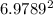`6.9789^(2)` = 48.7 or ≈ 49 (approx)

Therefore, sample size of at least 49 must be needed .