Question

A gas mixture consists of 4 kg of O2, 5 kg of N2, and 7 kg of CO2. Determine (a) the mass fraction of each component, (b) the mole fraction of each component, and (c) the average molar mass and gas constant of the mixture.

Answer 1

See explanation.

Step-by-step explanation:

Hello

(a) In this case, one uses the following formulas, which allow to compute the mass fraction of each component:
`\% O_2=(m_(O_2))/(m_(O_2)+m_(N_2)+m_(CO_2))*100\%=(4kg)/(4kg+5kg+7kg)*100\%=25\%O_2\\\% N_2=(m_(N_2))/(m_(O_2)+m_(N_2)+m_(CO_2))*100\%=(5kg)/(4kg+5kg+7kg)*100\%=31.25\%N_2\\\% CO_2=(m_(CO_2))/(m_(O_2)+m_(N_2)+m_(CO_2))*100\%=(7kg)/(4kg+5kg+7kg)*100\%=43.75\%CO_2`

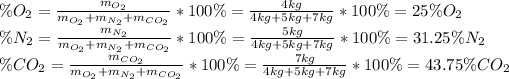
(b) For the mole fractions, it is necessary to find all the components' moles by using their molar mass as shown below:

`n_(O_2)=4kgO_2*(1kmolO_2)/(32kgO_2) =0.125kmolO_2\\n_(N_2)=5kgN_2*(1kmolN_2)/(28kgN_2) =0.179kmolN_2\\n_(CO_2)=7kgCO_2*(1kmolCO_2)/(44kgCO_2) =0.159kmolCO_2`

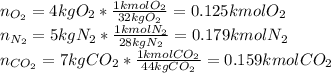
Now, the mole fractions:

`x_(O_2)=(n_(O_2))/(n_(O_2)+n_(N_2)+n_(CO_2))*100\%=(0.125kmolO_2)/(0.125kmolO_2+0.179kmolN_2+0.159kmolCO_2)*100\%=27\%O_2\\x_(N_2)=(n_(N_2))/(n_(O_2)+n_(N_2)+n_(CO_2))*100\%=(0.179kmolN_2)/(0.125kmolO_2+0.179kmolN_2+0.159kmolCO_2)*100\%=38.7\%N_2\\ x_(CO_2)=(n_(CO_2))/(n_(O_2)+n_(N_2)+n_(CO_2))*100\%=(0.159kmolCO_2)/(0.125kmolO_2+0.179kmolN_2+0.159kmolCO_2)*100\%=34.3\%CO_2`

(c) Finally the average molar mass is computed considering the molar fractions and each component's molar mass:

`M_(average)=0.27*32g/mol+0.387*28g/mol+0.343*44g/mol=34.57g/mol`

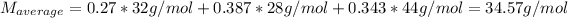
And the gas constant:

`Rg=0.082(atm*L)/(mol*K)*(1mol)/(34.57g)=0.00237(atm*L)/(g*K)`

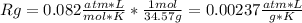
Best regards.