Question

A test consists of 10 true or false questions. To pass the test a student must answer at least eight questions correctly. If the student guesses on each question, what is the probability that the student will pass the test

Answer 1

The probability of any student passing the given test is 0.0538.

Explanation:

Here, the total number of questions in the test = 10

The minimum correct answers needed to pass the test = 8 or more

⇒ n ≥ 8

Now, since there are only 2 options for each question:

So, the probability of answering it right =
`((1)/(2) ) = 0.5 = p`

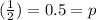
And the probability of answering it wrong =
`((1)/(2) ) = 0.5 = q`

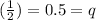
Now, let us use the Binomial Distribution Formula here:

`P(x) = ^nC_x p^xq^((n-x))`

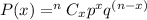
Now, solving for x = 8 , 9 and 10

When x = 8 , P(8) is given as :

`P(8) = ^(10)C_8 (0.5)^8(0.5)^((10-8)) = 45* (0.5)^8(0.5)^2 = 0.0439`

When x = 9 , P(9) is given as :

`P(9) = ^(10)C_9 (0.5)^9(0.5)^((10-9)) = 10* (0.5)^9(0.5)^1 = 0.009`

When x = 10 , P(10) is given as :

`P(10) = ^(10)C_(10) (0.5)^10(0.5)^((10-10)) = 10* (0.5)^(10)(0.5)^0 = 0.0009`

Now, adding the 3 probabilities, we get:

(P ≥ 8) = P(8) + P(9) + P(10) = 0.0439 + 0.009 + 0.0009 = 0.0538

or, (P ≥ 8) = 0.0538

Hence, the probability that the student will pass the test is 0.0538.