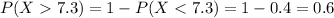Answer:
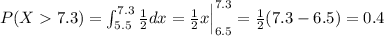
And then we can find the probability replacing the last result and we got:
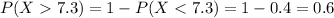
Explanation:
For this case we have the following density function given:
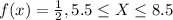
And we want to find the following probability:
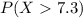
We can find this probability with the complement rule like this:
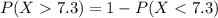
And we can find the following probability:
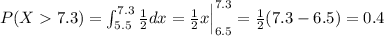
And then we can find the probability replacing the last result and we got: