Explanation:
To prove that:
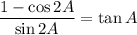
Let us take left hand side and prove it.
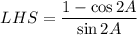
Using the trigonometric identity:
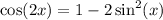
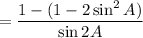
Using the trigonometric identity:
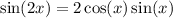
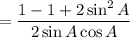
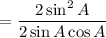
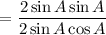
Cancel the common term 2 sin A on both numerator and denominator.
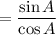
Using the trigonometric identity:
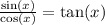
= tan A
= RHS
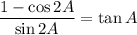
Hence proved.