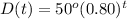Answer:
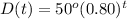
Explanation:
The correct question is
At the moment a hot cake is put in a cooler, the difference between the cake's and the cooler's temperatures is 50 degree Celsius. This causes the cake to cool and the temperature difference loses 1/5 of its value every minute.
Write a function that gives the temperature difference in degrees Celsius, D(t), t minutes after the cake was put in the cooler
we know that
The equation of a exponential decay function is equal to

where
D(t) is the temperature difference in degrees
t is the number of minutes
r is the rate of change
a is the initial value
we have
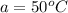
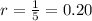
substitute