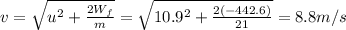Question

You get a running start, pushing a box of mass 21 kg up to a ramp of grade 0.7 and friction coefficient 0.48. The box has a speed 10.9 m/s when it starts up the ramp, the same time that you let it go. The ramp ends at a platform of height 3.14 m.(a) What is the work done by friction as the box goes up the ramp?(b) What is the speed of the box just before it hits the ground?

Answer 1

a) -442.6 J

b) 8.8 m/s

Step-by-step explanation:

a)

The work done by the friction force is equal to:

`W_f=-F_f d`

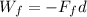
where

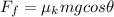`F_f = \mu_k mg cos \theta` is the frictional force on the box, where

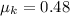`\mu_k = 0.48` is the coefficient of friction

m = 21 kg is the mass of the box

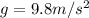`g=9.8 m/s^2` is the acceleration due to gravity

`\theta` is the angle of the ramp

The negative sign is due to the fact that the frictional force is opposite to the motion of the box

d is the length of the ramp

So the work can be rewritten as

`W_f=-\mu_k mg cos \theta d`

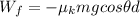
Here we know that the grade of the ramp, which is the ratio between height and horizontal length, is 0.7:

`grade=(h)/(L)=0.7`

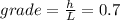
This means that

`tan \theta=0.7`

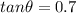
So we find the angle:

`\theta=tan^(-1)(0.7)=35.0^(\circ)`

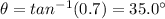
We also know that the height of the ramp is

h = 3.14 m

So we can find the length of the ramp:

`d=(h)/(sin \theta)=(3.14)/(sin 35^(\circ))=5.47 m`

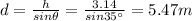
Therefore, the work done by friction is

`W_f=-(0.48)(21)(9.8)(cos 35^(\circ))(5.47)=-442.6 J`

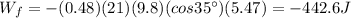
b)

The final speed of the box can be found by using the law of conservation of energy. In fact, the initial kinetic energy of the box (at the bottom) + the work done by friction must be equal to the final kinetic energy of the box, as it reaches the ground after leaving the platform.

So we can write:

`KE_i+W_f=KE_f\\(1)/(2)mu^2 + W_f = (1)/(2)mv^2`

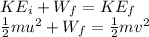
where:

u = 10.9 m/s is the initial speed of the box

m = 21 kg is the mass of the box

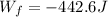`W_f=-442.6 J` is the work done by friction

`v` is the final speed of the box as it reaches the ground

Solving for v, we find:

`v=\sqrt{u^2+(2W_f)/(m)}=\sqrt{10.9^2+(2(-442.6))/(21)}=8.8 m/s`