Question

H function is even, odd, or neither.
b. g(x) = x² - 2
Is it odd or even

Answer 1

`g(x) = x^2 - 2 \text{ is even function }`

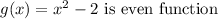
Solution:

Given that,

`g(x) = x^2 - 2`

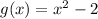
We have to find whether the above function is odd or even

If a function is: y = f(x)

If f(-x) = f(x), the function is even

If f(-x) = - f(x), the function is odd

Which is,

`\mathrm{Even\:Function:\:\:A\:function\:is\:even\:if\:}f\left(-x\right)=f\left(x\right)\mathrm{\:for\:all\:}x\in \mathbb{R}\\\\\mathrm{Odd\:Function:\:\:A\:function\:is\:odd\:if\:}f\left(-x\right)=-f\left(x\right)\mathrm{\:for\:all\:}x\in \mathbb{R}`

From given,

`g(x) = x^2 - 2`

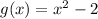
Replace x with -x

`g(-x) = (-x)^2 - 2\\\\g(-x) = x^2 - 2`

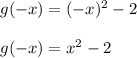
Therefore,

`g(x) = g(-x)`

Thus the function g(x) is even