Question

The value, V (t), in dollars, of a stock t months after it is purchased is modeled by the following equation.

V(t)= 42(1-e ^-1.5t) +36



a) V (1) =$_____________. (Round to two decimal places as needed)
V (12) =$______________.(Round to two decimal places as needed)

b)Find V '(t)=___________.(Simply your answer. Use intergers or decimal for any numbers in the expression. Round to one decimal place as needed)

c) After how many months will the value of the stock first reach $75?________( Do not round until the final answer. Then round to one decimal place as needed)

d)lim V (t)= $__________
t-->[infinity]

Answer 1

Explanation:
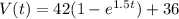`V(t)= 42(1-e ^(1.5t) ) +36` is given value in dollars of a stock in t months after it is purchased.

a) Substitute 1 for t

`V(1) = 42(1-e^(-1.5) )+36 \\=67.852\\=67.85`

V(12) =
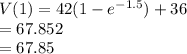
`V(1) = 42(1-e^(-1.5*12) )+36 \\=77.00`

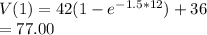
b) Find derivative for V

`V'(t) = 42(-1.5) e^(-1.5t) )\\\\=-63e^(-1.5t)`

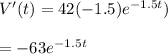
c) When V(t) = 75

`V(t)=75= 42(1-e ^(1.5t) ) +36\\1-e ^{1.5t=0.9286\\=-2.639`

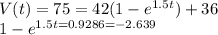
d) As t tends to infinity, exponent being in negative t tends to 0

So V tends to 42(1-0)+36 = 78