Complete Question
The diagram for this question is shown on the first uploaded image
Answer:
a E =

b E =
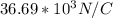
c E = 0 N/C
d
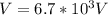
e
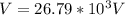
f V =

g
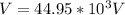
h
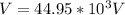
i
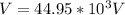
Step-by-step explanation:
From the question we are given that
The first charge
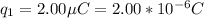
The second charge
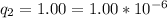
The first radius
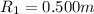
The second radius
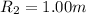
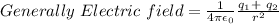
And
![Potential \ Difference = (1)/(4\pi \epsilon_0) [(q_1 )/(r)+(q_2)/(R_2) ]](https://img.qammunity.org/2021/formulas/physics/college/wizahm15v27ct9wqtjawmfbdddi1s5p69g.png)
The objective is to obtain the the magnitude of electric for different cases
And the potential difference for other cases
Considering a
r = 4.00 m
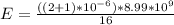
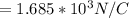
Considering b
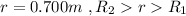
This implies that the electric field would be
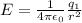
This because it the electric filed of the charge which is below it in distance that it would feel
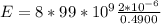
=
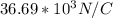
Considering c
r = 0.200 m
=>

The electric field = 0
This is because the both charge are above it in terms of distance so it wont feel the effect of their electric field
Considering d
r = 4.00 m
=>
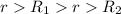
Now the potential difference is
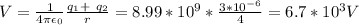
This so because the distance between the charge we are considering is further than the two charges given
Considering e
r = 1.00 m
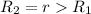
![V = (1)/(4\pi \epsilon_0) [(q_1)/(r) +(q_2)/(R_2) ] = 8.99*10^9 * [(2.00*10^(-6))/(1.00) (1.00*10^(-6))/(1.00) ] = 26.79 *10^3 V](https://img.qammunity.org/2021/formulas/physics/college/zeo17rgyd59chh1xb54torkukd364y922d.png)
Considering f
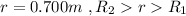
![V = (1)/(4\pi \epsilon_0) [(q_1)/(r) +(q_2)/(R_2) ] = 8.99*10^9 * [(2.00*10^(-6))/(0.700) (1.0*10^(-6))/(1.00) ] = 34.67 *10^3 V](https://img.qammunity.org/2021/formulas/physics/college/sq7teu2j9jq2rr3jq0o5k5w5rgfk1hk6hf.png)
Considering g
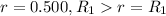
![V = (1)/(4\pi \epsilon_0) [(q_1)/(r) +(q_2)/(R_2) ] = 8.99*10^9 * [(2.00*10^(-6))/(0.500) (1.0*10^(-6))/(1.00) ] = 44.95 *10^3 V](https://img.qammunity.org/2021/formulas/physics/college/l4bcp6bf3z3kfuoq5tzei45g6nrnl7imez.png)
Considering h
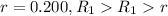
![V = (1)/(4\pi \epsilon_0) [(q_1)/(R_1) +(q_2)/(R_2) ] = 8.99*10^9 * [(2.00*10^(-6))/(0.500) (1.0*10^(-6))/(1.00) ] = 44.95 *10^3 V](https://img.qammunity.org/2021/formulas/physics/college/f5qa6iywuzu07dxvy1xqgvdzqr2633s5kg.png)
Considering i
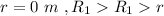
![V = (1)/(4\pi \epsilon_0) [(q_1)/(R_1) +(q_2)/(R_2) ] = 8.99*10^9 * [(2.00*10^(-6))/(0.500) (1.0*10^(-6))/(1.00) ] = 44.95 *10^3 V](https://img.qammunity.org/2021/formulas/physics/college/f5qa6iywuzu07dxvy1xqgvdzqr2633s5kg.png)