Answer:
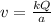
Step-by-step explanation:
We define the linear density of charge as:
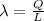
Where L is the rod's length, in this case the semicircle's length L = πr
The potential created at the center by an differential element of charge is:

where k is the coulomb's constant
r is the distance from dq to center of the circle
Thus.
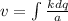

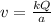 Potential at the center of the semicircle
Potential at the center of the semicircle