Answer:
(a) The sample size required is 2401.
(b) The sample size required is 2377.
(c) Yes, on increasing the proportion value the sample size decreased.
Explanation:
The confidence interval for population proportion p is:

The margin of error in this interval is:

The information provided is:
MOE = 0.02
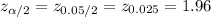
(a)
Assume that the proportion value is 0.50.
Compute the value of n as follows:

Thus, the sample size required is 2401.
(b)
Given that the proportion value is 0.55.
Compute the value of n as follows:

Thus, the sample size required is 2377.
(c)
On increasing the proportion value the sample size decreased.