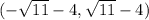Question

Solve the inequality and express your answer in interval notation
x^2+8x+5 <0

Answer 1

The interval notation is
`(-√(11)-4, √(11)-4)`

Step-by-step explanation:

The inequality is
`x^(2)+8 x+5<0`

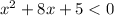
Let us complete the square, we get,

`x^(2)+8 x+5+4^(2)-4^(2)<0`

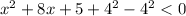
Simplifying, we have,

`(x+4)^(2)+5-4^(2)<0`

`(x+4)^(2)-11<0`

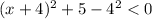
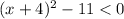
Adding both sides of the equation by 11, we get,

`(x+4)^(2)<11`

Since, we know that for
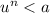`u^(n)<a` , if n is even then
`-\sqrt[n]{a}<u<\sqrt[n]{a}`

Thus, writing the above expression in this form, we get,

`-√(11)<x+4<√(11)`

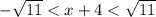
Also, if
`a<u<b` then
`a<u` and
`u<b`

Then ,we have,

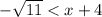`-√(11)<x+4` and
`x+4<√(11)`

Solving the inequalities, we get,

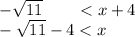`-√(11)\ \ \ \ \ \ <x+4\\-√(11)-4<x` and
`x+4<√(11)\\x \ \ \ \ \ <√(11)-4`

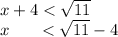
Merging the intervals, we have,

`-√(11)-4<x<√(11)-4`

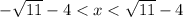
Hence, writing the solution in interval notation, we have,

`(-√(11)-4, √(11)-4)`

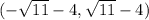
Therefore, the answer is
`(-√(11)-4, √(11)-4)`