Question

On a test with a population mean of 75 and standard deviation equal to 16, if the scores are normally distributed, what percentage of scores fall between 70 and 80?

Answer 1

Percentage of scores that fall between 70 and 80 = 24.34%

Explanation:

We are given a test with a population mean of 75 and standard deviation equal to 16.

Let X = Percentage of scores

Since, X ~ N(
`\mu,\sigma^(2)`)

The z probability is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1) where,
`\mu` = 75 and
`\sigma` = 16

So, P(70 < X < 80) = P(X < 80) - P(X <= 70)

P(X < 80) = P(
`(X-\mu)/(\sigma)` <
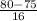`(80-75)/(16)` ) = P(Z < 0.31) = 0.62172

P(X <= 70) = P(
`(X-\mu)/(\sigma)` <
`(70-75)/(16)` ) = P(Z < -0.31) = 1 - P(Z <= 0.31)

= 1 - 0.62172 = 0.37828

Therefore, P(70 < X < 80) = 0.62172 - 0.37828 = 0.24344 or 24.34%